Oh boy time for an update!
Today we’ll be introducing multiple species into the same patch and simulating them coexisting.
They won’t eat or fight each other yet, that will come in a later update. Instead we will make them compete
over compounds by racing to get there first. In this update I will explain the math behind this to you, and show you the results.
To be entirely honest, I don’t understand exactly what Nick did here or whether it was correct, so instead I started from scratch.
I put all the math stuff in a spoiler to prevent this post from bloating, but basically:
- Competition occurs when multiple organisms (not just multiple species! ) are attempting to gather the same type of cloud.
- Competition causes organisms to waste time, because sometimes the compound cloud they were hunting has already been eaten by another microbe. This happens even when both microbes are of the same species, and even when there is no shortage of food at all.
- In times of shortage it also causes some species to take home a larger share of food than the others, resulting in unequal amounts of starvation. In the long run we would expect this to make suboptimal species go extinct when a more optimal species is hunting the same type of cloud.
Math stuff
First let’s consider a scenario with only one species. In this case the species would need a certain amount of clouds, and there would be a certain amount of clouds in the patch. If there are more clouds in the patch than the species needs everything is fine. In that case the species would have a success probabilty of 1. There might be some issues where two individuals go for the same cloud and one ends up wasting some time before it goes to a different cloud, but eventually it will find a cloud that no one else ate. The only thing the species can stand to lose is time.
That changes when the species needs more clouds than the patch contains; there’s a shortage!
In this case the species only achieves a success probability of clouds / hunts required (in addition to wasting time as before).
This success probability formula might break down if we introduce another species to the patch, because the species will have to compete. The total fraction of hunts that are succesfull is still clouds / total hunts required, but each species individually only contributes some fraction of the hunts. If both species are equally matched, and require an equal number of hunts this fraction will be 1/2, giving each species half of the total clouds. But that will almost never be the case. Most species will be either unequally matched, or one species will need more of a given compound than the other.
Let’s imagine the latter case first. In this case we would expect each species to take a fraction of the clouds proportional to how many clouds they require. This already happens given our current formula:
sucessfull hunts = clouds / hunts required * 1/2.
Now let’s imagine what might happen if the competition between species isn’t even:
What if one species is faster? What if there is a third species upsetting the balance?
For this I will use an abstraction that has served me fairly well in estimating probabilities in the past. We will give each species a competitiveness rating. For now we’ll set it equal to speed, since that is the primary determiner of who gets to the clouds first. Using speed = competitiveness is just a guess, but finding the actual value would require icky stuff like game theory.
Next we add up all the competitiveness ratings of all the species to find the total competition in the patch.
Finally we replace the 1/2 in the formula with competitiveness / total competition. This gives us:
success probability = (clouds / hunts required) * (competitiveness / total competition)
clouds gathered = hunts required * success probability.
But what about that wasted time I mentioned earlier? How will we calculate the amount of time per hunt, given the amount of competition?
This depends on the time per hunt the algorithm already calculates, and the amount of times a microbe has to try before he finds a cloud that he can actually get. So how many tries does it take on average to find such a cloud? Well I can’t disguise the probability theory we need for that as simple math so hold on to your butts.
Assume that each microbe picks a random cloud to swim to. Irl they would of course pick the closest cloud, but the position of the microbe is random, and the position of the cloud is random, so who cares. A competition occurs when at least two hunts are for the same cloud.
The chance that any given hunt is for the same cloud as you = 1 / clouds.
The chance that it is not not for the same cloud = 1 - 1 / clouds.
The chance that every single hunt does not pick the same cloud = (1 - 1 / clouds)^hunts
Thus, the chance that at least one other microbe picks the same cloud = 1 - (1 - 1 / clouds)^hunts.
If a microbe gets into a competition and wins, he does not waste any time; that only happens if he loses.
The chance that a microbe wins his competition = competitiveness / total competition based on the abstraction from earlier.
Thus the chance that they lose = 1 - competitiveness / total competition.
Except that in the case of wasting time, losing to your own species also counts, increasing the chance of a loss.
Therefore we add the species’ own competitiveness to the competition:
chance of losing = 1- competitiveness / (competitiveness + total competition).
The chance that they get into a competition is simply both probabilities multiplied.
Some fraction of microbes will have the opportunity to try again after losing a competition, wasting time; their competition was caused by inefficiency, not by a shortage. The chance that this happens = 1 - (hunts required - clouds / hunts required). The average amount of tries would then be: 1 + chance of competition * chance of losing * chance of retrying. Except there’s no guarantee that the microbe won’t lose again and do a retry of a retry. Or a retry of a retry of a retry! You might think that we’ve found an unsolvable infinite loop, and you’d be partially correct. It is an infinite loop. It’s not unsolvable. This monstrosity we’ve created is called a geometric series. Google it if you want to know how I got this solution:
average amount of tries = 1 / (1 - chance of competing * chance of losing * chance of retrying).
This gives us all the information needed to start making microbes compete with each other.
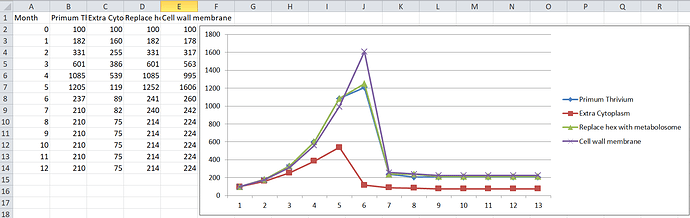
The first thing I did was ran 3 tests to verify that the system works even in weird scenarios:
-
I ran the exact same scenario as last time. This gives a slightly lower population than last time, but only as much lower as can be explained as intraspecific competition. This proves our changed algorithm gives the exact same result as the old algorithm given no competition.
-
I divided Primum Thrivium in two. Both halves of Primum Thrivium are exactly the same kind of microbe, I just arbitrarily declared that they are two different species. The result is that both species have an identical population: half of what they would have had if they were still one species. This proves that the simulation does not favour any individual microbe based on what species they belong to.
-
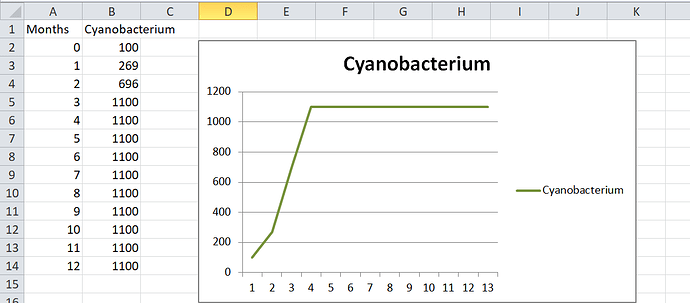
I introduced a second species, that does not compete with Primum Thrivium in any way. They have a completely separate food source. The result is that they have the exact same population they would have had if they were the only species in existance. This proves that the changes of the algorithm only apply when two species would realistically interact.
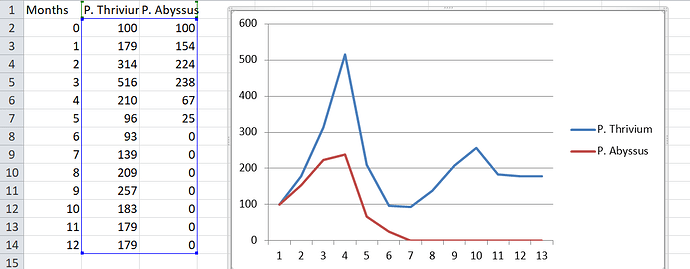
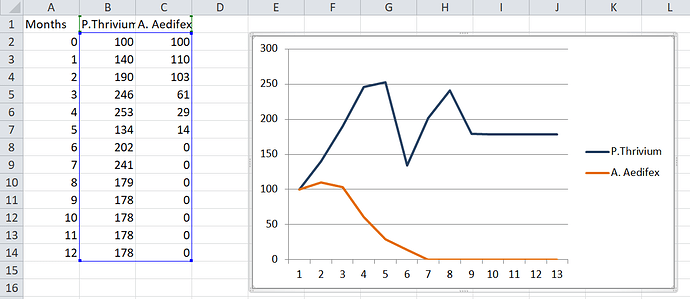
Now for the graphy stuff! If any of you have scenario’s you’re interested in let me know but here is one I came up with: We have two species, Primum Thrivium and Primum Abyssus (two hexes of cytoplasm with a single membrane). Both of them compete for glucose.
P. Thrivium immediately has an edge due to being faster, which allows them to get to the glucose first. Despite this they eat less glucose in total, because they need less. Thus, it is Abyssus who causes the food to run out, and Abyssus who pays the price. Thrivium then starts growing again, but quickly runs into his own food shortage, settling into an equilibrium population just before the simulation ends.
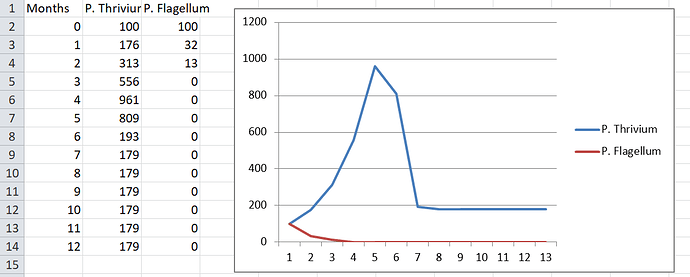
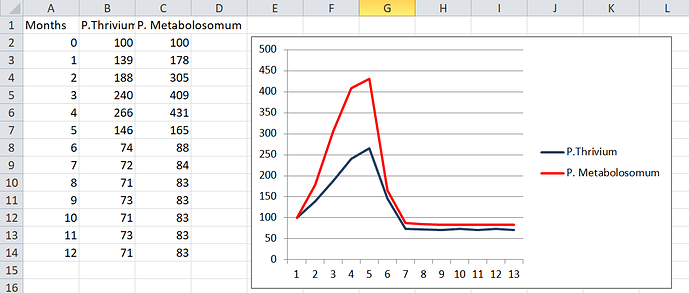
Second graphy thing! This time we pit P. Thrivium against P. Flagellum (one metabolosome and one flagellum). P. Flagellum needs way more glucose to survive, but is also way better at competing. Place your bets everyone!
F in the replies for P. Flagellum, who was unable to even gather enough glucose in a month to sustain themselves. Even if there was no competition they would have died within a couple months. P. Flagellum’s natural habitat would have to be very glucose rich. That said, I do think it’s a good thing that the algorithm is harsh on species like this. It shows that it actually knows what species are suboptimal in the game.
Meanwhile P. Thrivium is just chilling, barely noticing that P. Flagellum was ever there.
I’ll see you in the next update, where reproduction will work just like in the real game. Microbes won’t just have to compete for food, but also for phosphate, and ammonia!