What have they done again?
Watch the video to find out
2 Likes
If I ever become that rich and powerful, I’ll make Nintendo pay.
1 Like
F_0 = \dfrac{1}{4\pi\epsilon_0}\dfrac{|Q_1||Q_2|}{r^2}
1 Like
Is that equation for defeating Nintendo?
1 Like
Attraction of charges or bodies? I wonder.
3 Likes
I wonder if Twilight will show up on Christmas…
I finally remembered to turn on the Santa hats (thanks to people pinging me about it being my anniversary).
5 Likes
Guess the thrivesmas period has begun.
2 Likes
Does it though? If you divide a positive number by a smaller and smaller positive number the limit is obviously infinity, but there’s other kinds of numbers. Dividing the same number by a smaller and smaller negative number gives a totally different limit, negative infinity. This means we don’t know the sign of our answer. The limit of dividing by zero is +/-infinity, which is two answers, which isn’t really a limit, it’s supposed to converge, not diverge. except there’s a third answer. 0. If you divide zero by smaller and smaller numbers, either positive or negative, you approach 0. So, we approach infinity, negative infinity, and zero, all at once. I wouldn’t call that a limit. It’s undefined for a reason.
2 Likes
The keyword is “limit equation” which has different infinity rules than normal equations. I can’t remember that much math after years of not using most of it, but I think limit equations can very easily and often converge on an infinity even if the limit it approaches is (causing) a division by zero.
2 Likes
I’d think dividing 0 by 0 would result in 1, since that’s what other numbers do when divided by themselves.
0/0 is not one. What is one divided by negative one (x/-x for any real x)? it’s negative one. Again, sign matters, and zero does not have an ordinary sign. If zero is of equal sign with itself, you’d be right, but with it’s lack of a sign, 0/0 is in a superposition of +/- 1. or is it? Because if you divide 0 by smaller and smaller numbers, negative or positive, you always get 0. Just like any number divided by zero, we’re stuck with three answers, it’s just replaces infinity with one. If you have three answers, you don’t have an answer, which is what we are looking for. Again, undefined for a reason.
You’re totally right, but I don’t think that applies to the general case of x/0. think of these two graphs.
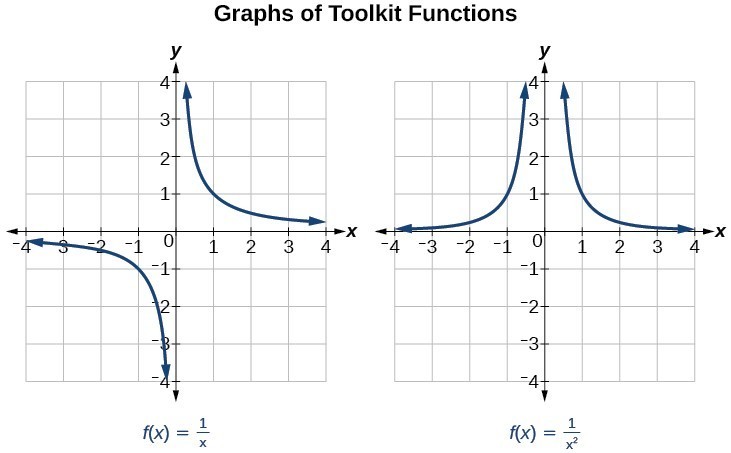
Both have a division by zero but the limit exists only for one of them because x^2 is always positive while x can be of either sign. 1/0^2 isn’t any saner of a statement than 1/0, but 1/0 has two directions you can approach it from that have wildly different logical limits, while 1/0^2 kinda just has the one logical limit.
3 Likes
New poll time
When have you last seen a mosquito?
- 1 hour ago
- 6 hours ago
- 1 day ago
- 1 week ago
- 2 weeks ago
- 1 month ago
- Even earlier
0
voters
1 Like
Oh hey we got little hats again.
4 Likes
You belong to West facing hats, one of us, me, hh. Welcome.
Unless it’s different each client
2 Likes
It’s different based on the visible post index so it’s going to change for you a lot as well.
3 Likes
Can’t wait until forward-facing hats
1 Like
Take any 2 
–this message too short–